Watering the neurons
Joe wrote:
- Greg wrote:
-
i have proven physicalism true with a theorem of logic
(x){[(B)Bx->Mx]&(Mx->Pa)& (~Hx>~Rx)}->(x){[(B)Bx&(B=C)]->[(Cx->Mx )->Pa]}
the (B)Bx means x has property B, Mx means x has a material aspect to consciousness (could be made more explicit) and Pa is a constant signifying physicalism. the not Hx and not Rx stand for if you don't have a hippocampus you don't have episodic memory. the Cx stands for X is conscious.
"Pa" is a singular statement - not a "constant". "a" is the constant. The statement "Pa" means that one thing, "a", in the universe is physical or that "a" can be interpreted as falling-under the property of physicalism. Physicalism is more elastic - than your cashing it out, as having "a material aspect to conscious". Physicalism proposes that nothing but physical events exist in the universe or that any event which exists can be ultimately reduced to its physical properties. To physicalists - if consciousness were not entirely fictitious or a poetic means of expressing our subjective experiences - trivially there could be nothing but "a material aspect to consciousness". From a physicalist's point of view, your "theorem" is redundant.
The phrase "has a material aspect" is vague (or worse). Does the moon: a macroscopic object, a quark: a microscopic object, a gamma ray: a burst of high-frequency electromagnetic radiation and a human memory contain this "material aspect" - univocally; that is, in the same sense? It's rather curious that a physicalist would use the phrase "has a material aspect" - because according to physicalists, there is no aspect other than the material. The use of the phrase "material aspect" by a physicalist is roughly comparable to a solipsist maintaining that "The tree over there has a my mind aspect.". To a solipsist, nothing but his mind exists, and no thing could have other than a his-mind-aspect to it.
The conditional "~Hx>~Rx" can be translated as: "If x lacks a hippocampus, then x lacks episodic memory." The statement is a universal generalization - because the variable is bound by the all operator "(x)". Only one counter-example is required to defuse a universal generalization. If one person is found to lack a hippocampus but has episodic, i.e. long-term memories, then the conditional "~Hx>~Rx" is false.
Compare the following images. On the left, the region of the brain where the hippocampus is located is known as the "medial temporal lobe". On the right, a hydrocephalus (water on the brain) patient lacks neural matter in his "medial temporal lobe"; hence, he has no hippocampus. The "medial temporal lobe" is among the first sectors of the brain to be wiped-out by the congestion of cerebro-spinal fluid - because it's located (in close proximity) to where the spinal cord enters the brain.
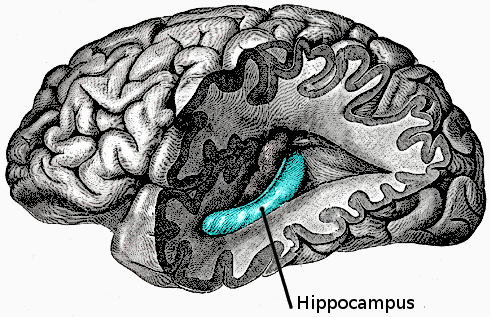

Not only is the conditional "~Hx->~Rx" un-necessary for physicalism, it's not true. There are extreme cases of hydrocephalus - in which patients lose 50% or so of their brain mass, but - due to neuro-plasticity, many of their functions shuffle-around and are re-localized in the remaining viable sectors of their brains. In these patients, there's a thin slice of neurons running-along the inner diameter of their skulls - the only portion of their brains left undamaged. However, these patients do not recover fully. For example, they lack co-ordination and generally register low IQs, yet - to most observers, hydrocephalus sufferers appear base-line (nominally) functional. These patients lack a hippocampus region (the medial temporal lobe) in their brains, but they do have episodic, i.e. long-term memory. Declaring that this or that brain organ to be uniquely associated with memory (or another faculty) does not get the theory of physicalism off the ground.
Neuro-plasticity: When a region of the brain is destroyed, an intact, yet spatially distinct region can co-opt the function of the region which was destroyed. Other phrases used to describe this mechanism are "the recovery of function" and "the re-localization of function". Neuro-plasticity proves that a specific sector of the brain is not hard-wired to perform a specific brain function. 50 years ago or so, the brain was conjectured to be hard-wired. But, the brain is not hard-wired, and - when a region of the ancient cortex (the hippocampus) is eliminated by fluid, its functions can (and usually do) migrate to the neo-cortex (or another part of the brain).
In first order logic, the expression "B=C" makes no sense. How can property "B" and property "C" be identical? In first order logic - which contains the axiom of identity, individuals (values or variables) can be indentical (inter-substitutable in a statement), but properties cannot be. Identity in first order requires that all of the properties which (generally 2) persons, places, things, etc. have be identical, i.e. Leibniz's law. But - under first order logic, properties, themselves, cannot be identical to each other. "B" and "C", cannot be inter-substitutable for each another. "B=C" should be thrown-out.
Finally, "(B)Bx means x has property B". No. "Bx" means that x has property B. In first order logic, "(B)Bx" means nothing. The statements below are - probably - how you meant to symbolize the "theorem" in first-order logic - without illicitly quantifying-over non variables and attempting to make non-identical properties indiscernable.
A(x)[ (Hx & Cx & Mcx) -> Pc ]
For every x, if x is a human and x has consciousness and consciousness is materially related to x, then consciousness falls-under a physicalist explanation.
Or stronger:
A(x)[ (Hx & Cx & Mcx) & -E(y)[ Hy & Cy & -Mcy ] & x=y -> Pc ]
For every x, if x is a human and x has consciousness and consciousness is materially related to x, but it is false that there is a y; such that, y is a human and y has consciousness but consciousness is not materially related to y and x is identical to y, then consciousness falls-under a physicalist explanation.